What is root mean square error RMSE and MSE

In machine learning and more specifically in supervised learning, it is important to have a metric that indicates the error that our model has. There are different metrics that give us an idea of ​​how good or bad our prediction model is.

One of them is the MSE (Mean Squared Error) or the RMSE (Root Mean Squared Error). The second differs from the first in that the square root is used to obtain the units of the problem instead of having them squared.

The calculation of MSE or RMSE consists of comparing the actual values ​​with those predicted by the model. This comparison is made through the Euclidean distance of both values.

In the following image we can see a linear regression (blue line) and the actual data points (yellow color). For each point we see a red line that connects with the model point, in this case with the linear regression line. The red line represents the Euclidean distance between both points. This is calculated by operating the norm on the difference of the values.

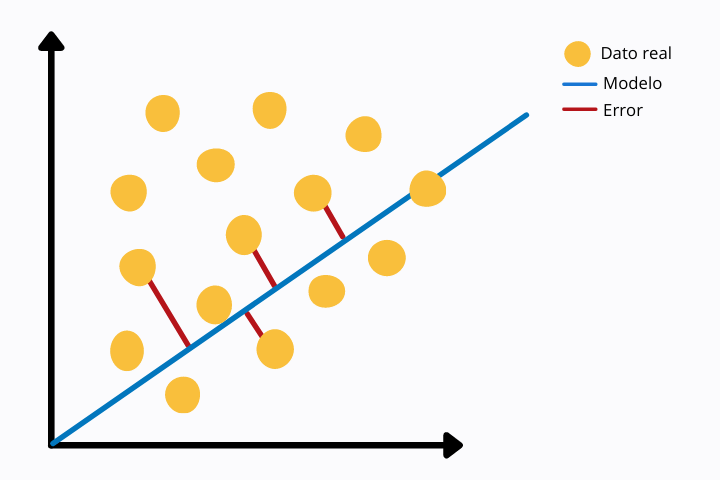
This error metric is more sensitive to outliers since we are using a power. Other measures less sensitive to outliers are, for example, the MAE or Mean Absolute Error in which the absolute value is taken without squaring it.

During the training of the machine learning model in supervised learning, in each iteration an error function is calculated that is then minimized through optimization algorithms with the aim of reducing the error and improving the result with each iteration.

There are multiple error functions (also known as cost functions). One of them is the MSE or Mean Square Error.

This function has the shape of a parabola so it only has a global minimum. This feature makes it ideal for minimization algorithms as they will more easily find the global value that minimizes the error without getting trapped in other local minima.

The RMSE is more intuitive than the MSE, but at a computational level it is more expensive. In supervised learning such as neural network architectures, the error has to be calculated in each iteration. For this reason, since RMSE is more expensive, it is preferable to use MSE as a cost function.

Another reason is that the gradient descent optimization algorithm has better performance over MSE than over RMSE.

As we have seen, MAE is an error metric very similar to MSE or RMSE. MAE is more robust than RMSE and therefore does not give as much importance to outliers. Otherwise, RMSE, by raising the absolute value of the difference to the square, gives more importance to the outliers.

RMSE and MSE are differentiable functions so they can be used in optimization problems. Furthermore, at each point the gradient is different, that is, the first derivative with respect to the error function varies point by point. This does not happen in the case of the MAE function where the gradient is the same at each point, except at zero where it is not differentiable. The derived function is not continuous throughout the domain.

This can cause problems when training the model, especially when we use neural networks.

In some problems it is possible that neither RMSE, MSE or MAE will help us. In this case we will have to look for alternatives. One of them is the loss function known as the Huber function.

It is a piecewise function that is robust to outliers and is differentiable to 0 unlike MAE.

The Huber function has an adjustable delta parameter that has to be tuned depending on the problem of interest.

Another alternative to traditional cost functions is the Log-Cosh function. This is similar to the mean square error with the difference that it is softer, making it less sensitive to outliers.

Furthermore, the function is doubly differentiable unlike the Huber function which is only differentiable once.

As it has a double derivative, the Log-Cosh function can be used by second-order optimization methods, such as the Newton-Raphson method, used in optimization techniques. gradient boosting like XGBoost.