Dirac equation, discover the meaning of this formula that mixes quantum with relativity

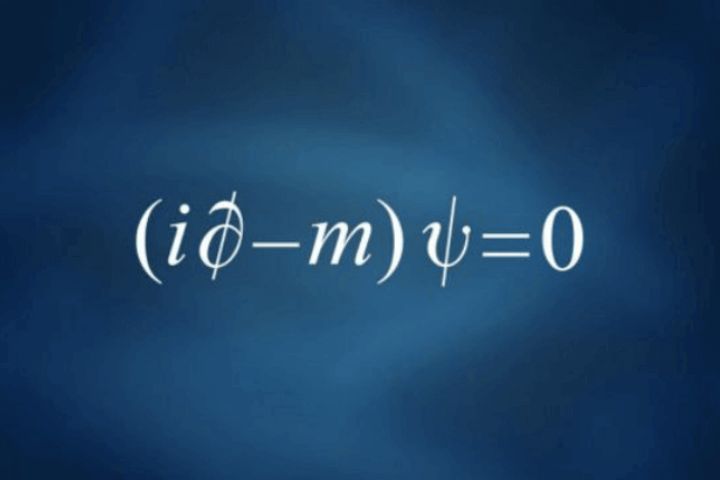
The Dirac equation, also known as the love equation or the most beautiful equation in the world for its simplicity, is a fundamental equation in physics that combines quantum mechanics and the theory of relativity to describe particles with spin 1/2, such as electrons, taking into account relativistic effects and predicting the existence of antiparticles.

Do you want to discover more about this beautiful formula?

Stay with us and discover why Paul Dirac has been one of the great physicists of the 20th century!

During the 20th century, two of the most influential theories in modern physics emerged: general relativity and quantum mechanics. These two beautiful theories allow us to describe the majority of physical phenomena in our universe.

The laws of quantum mechanics explain to us what happens in the smallest world, the atomic and subatomic world. Instead, Einstein's general relativity teaches us what happens in the larger world, that of stars and galaxies.

There were some drawbacks. Electrons, as we have said, followed Schrödinger's wave quantum mechanics. However, when electrons acquire very high speeds, close to the speed of light, the effects of special relativity begin to be important.

The Schrödinger equation describes NON-relativistic quantum particles.

As Einstein taught us, space and time are sides of the same coin, space-time. The Schrödinger equation treats space and time differently since time is in a partial derivative of order 1, while space is in the form of a partial derivative of order 2.

So how can we describe relativistic quantum particles?

Paul Dirac was the one who solved this problem by converting Schrödinger's wave equation into a relativistic equation. We all know Einstein's famous equation E=mc^2, surely the most famous equation in history.

Well, it turns out that we can merge this equation with the Schrödinger equation, obtaining the Klein-Gordon equation that describes the behavior of a quantum particle with relativistic effects.

However, this expression had certain problems. This expression has the derivative with respect to time squared.

As we know from basic mathematics, an equation of order 2 has two solutions. In this case, the second equation represents a negative energy.

But... What does negative energy physically represent?

Another problem with the Klein-Gordon equation is that negative probabilities are obtained with the squared wave function. But as we know from Max Born, the square of the wave function represents the probability of finding the particle in a defined region.

Therefore, negative probabilities have no real physical meaning.

What did Dirac do to solve these problems?

Easy, I have removed the squares from the equation and problem solved.

Well… it's actually much more complex than that.

He thought of a mathematical expression that squared would be equivalent to the Klein-Gordon equation.

This new equation depended on parameters that Dirac found to be matrices.

Now comes the magic...

These 4x4 matrices (Dirac matrices) had the famous Pauli implicit matrices.

Don't you know what Pauli matrices are?

My mother...

Well, the Pauli matrices are the irreducible representation of the Lie group SU(2). A symmetry group that describes the spin of a particle.

Still don't understand anything?

Let's make it easier...

Pauli matrices are the mathematical objects that describe the spin of quantum particles.

Better?

We continue…

Dirac said that spin is nothing more than the consequence of applying relativistic laws in the quantum world.

In this equation the wave function no longer has the properties of a vector. These different properties describe a more complex mathematical object, a spinor.

The spinor that describes the wave function is a column matrix with 4 components. This gives us two results. One of them with negative energy.

How is this interpreted?

Dirac interpreted this result as solutions belonging to analogous particles with opposite charge to the original particle. He called them antiparticles.

Well yes…

Antimatter is born naturally from the Dirac equation. Years later, the existence of antielectrons known as positrons was experimentally demonstrated. Later the existence of antineutrons and antiprotons was also confirmed.

Do you realize everything that this beautiful and beautiful equation implies?

We have seen what the Dirac equation is and some of its implications in modern physics. But if you still haven't had enough and you're into hardcore, now we'll start with the interesting part. The mathematical formulation of the most beautiful equation in history, the Dirac formula.

On the left of the equation we have the relativistic energy equation: E^2 = p^2c^2+m^2+c^4 and on the right the definition of the energy operator of the Schrödinger equation.

In this way the Klein-Gordon equation is obtained. However, as we have previously mentioned, this expression presents certain difficulties that are incompatible with the foundations of quantum mechanics.

The trick that Dirac applied (as we see in the following equation) was to find a mathematical expression that squared was equivalent to the Klein-Gordon equation.

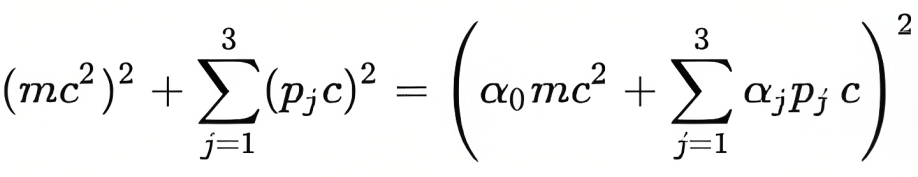
This expression depends on two parameters that Dirac found to be matrices and not real or complex numbers.

Developing the equations and using covariant relativistic notation we arrive at the famous Dirac equation: (∂ - m) ψ = 0.

The relativistic equation for energy in principle accepts both positive energies and negative energies.

But... What is negative energy?

In our experience, negative energies do not exist, but Dirac gave an interesting explanation that would resolve this apparently impossible negative solution.

He said that the void would have all the negative energy states occupied. This model is known as the Dirac ocean or sea, which considers the state of the vacuum as an infinite sea of ​​electrons with negative energy.

Any extra electron would have to occupy a positive energy state since the Pauli exclusion principle prohibits two fermions from occupying the same quantum state.

Later Dirac said that if they were not all complete, there would be a “gap” in one of the negative energy states and this would behave like a positively charged particle.

This particle was the positron (the antiparticle of the electron) which was later discovered experimentally by Carl David Anderson.