Qué es el error medio cuadrático RMSE y MSE

En machine learning y más concretamente en aprendizaje supervisado és importante tener una métrica que nos indique el error que tiene nuestro modelo. Existen distintas métricas que nos dan una idea de lo bueno o malo que es nuestro modelo de predicción.

Una de ellas es el MSE (Mean Squared Error) o el RMSE (Root Mean Squared Error). El segundo se diferencia del primero en que se utiliza la raíz cuadrada para obtener las unidades del problema en vez de tenerlas elevadas al cuadrado.

El cálculo de MSE o RMSE consiste en comparar los valores reales con los predichos por el modelo. Esta comparación se hace a través de la distancia euclidea de ambos valores.

En la siguiente imagen podemos ver una regresión lineal (línea azul) y los puntos de datos reales (color amarillo). Para cada punto vemos una línea roja que une con el punto del modelo, en este caso con la recta de la regresión lineal. La línea roja representa la distancia euclidea entre ambos puntos. Esta se calcula operando la norma sobre la diferencia de los valores.

Recomendado

Inteligencia Artificial en Medicina

La inteligencia artificial puede mejorar muchos aspectos del sector de la salud y medicina. Te mostramos 5 aplicaciones en que la IA se aplicará en la medicina.

Ver artículo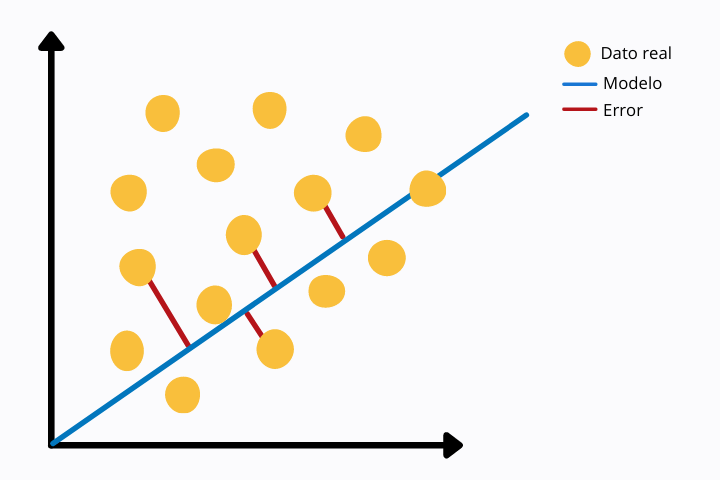

Esta métrica de error es más sensible a valores atípicos o outliers ya que estamos utilizando una potencia. Otras medidas menos sensibles a outliers son por ejemplo el MAE o Error Absoluto Medio en el cual se realiza el valor absoluto sin elevarlo al cuadrado.

Durante el entrenamiento del modelo de machine learning en aprendizaje supervisado, en cada iteración se calcula una función de error que luego es minimizada a través de algoritmos de optimización con el objetivo de reducir el error e ir mejorando el resultado a cada iteración.

Existe múltiples funciones de error (también conocidas como función de coste). Una de ellas es el MSE o Error Cuadrático Medio.

Esta función tiene forma de parábola por lo que solo tiene un mínimo global. Esta característica hace que sea ideal para los algoritmos de minimización ya que encontrarán más fácilmente el valor global que minimiza el error sin quedarse atrapada en otros mínimos locales.

El RMSE es más intuito que el MSE, pero a nivel computacional es más costoso. En aprendizaje supervisado como arquitecturas de redes neuronales el error tiene que ser calculado en cada iteración. Por esta razón, al ser RMSE más costoso es preferible usar MSE como función de coste.

Otra razón es que el algoritmo de optimización de descenso del gradiente tiene un mejor rendimiento sobre MSE que sobre RMSE.

Cómo hemos visto, MAE es una métrica de error muy parecida a MSE o RMSE. MAE es más robusto que RMSE y por lo tanto no les da tanta importancia a los valores atípicos. De lo contrario, RMSE, al elevar el valor absoluto de la diferencia al cuadrado otorga más importancia a los outliers.

RMSE y MSE son funciones diferenciables por lo que pueden ser usadas en problemas de optimización. Además, en cada punto el gradiente es diferente, es decir, la primera derivada con respecto la función de error varia punto a punto. Esto no sucede en el caso de la función MAE donde el gradiente es el mismo en cada punto, excepto en cero donde no es diferenciable. La función derivada no es continua en todo el dominio.

Esto puede generar problemas a la hora de entrenar el modelo, especialmente cuando usamos redes neuronales.

En algunos problemas es posible que no nos sirva ni RMSE, MSE o MAE. En este caso tendremos que buscar alternativas. Una de ellas es la función de perdida conocida como función de Huber.

Se trata de una función a trozos que es robusta a valores atípicos y que es diferenciable a 0 a diferencia de MAE.

La función de Huber tiene un parámetro ajustable delta que tiene que se tuneado dependiendo del problema de interés.

Otra alternativa a las funciones de coste tradicionales es la función Log-Cosh. Esta es parecida al error medio cuadrático con la diferencia de que es más suave, haciendo que sea menos sensible a los outliers.

Además, la función es doble diferenciable a diferencia de la función de Huber que solo es diferenciable una sola vez.

Al tener doble derivada, la función Log-Cosh puede ser empleada por métodos de optimización de segundo orden, como el método de Newton-Raphson, empleado en técnicas de gradient boosting como XGBoost.