Ecuación de Dirac, descubre el significado de esta fórmula que mezcla la cuántica con la relatividad

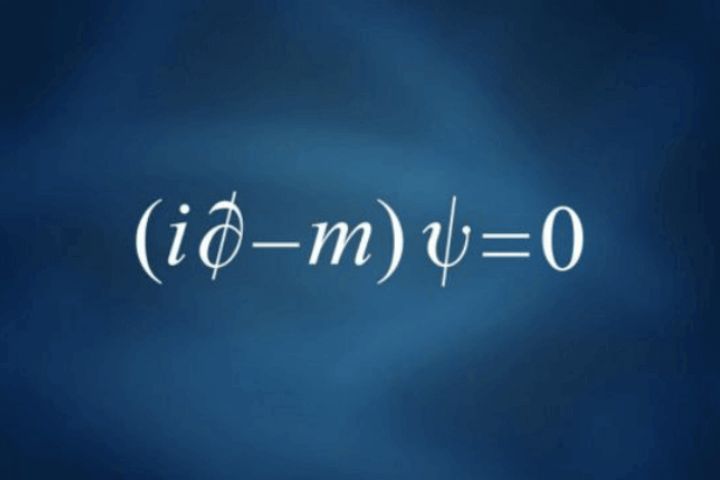
La ecuación de Dirac, también conocida como la ecuación del amor o la ecuación más bella del mundo por su simplicidad, es una ecuación fundamental en la física que combina la mecánica cuántica y la teoría de la relatividad para describir partículas con espín 1/2, como los electrones, teniendo en cuenta efectos relativistas y prediciendo la existencia de antipartículas.

¿Quieres descubrir más sobre esta preciosa formula?

¡Quédate con nosotros y descubre porque Paul Dirac ha sido uno de los grandes físicos del siglo XX!

Recomendado

Espacios de Hilbert

Los espacios de Hilbert son espacios vectoriales muy importantes en campos de la física como la cuántica. Descubre que son y sus propiedades.

Ver artículo

Durante el siglo XX surgieron dos de las teorías más influyentes en la física moderna: la relatividad general y la mecánica cuántica. Estas dos bellas teorías nos permitan describir la mayoría de fenómenos físicos de nuestro universo.

Las leyes de la mecánica cuántica nos explican lo que sucede en el mundo más pequeño, el mundo atómico y subatómico. En cambio, la relatividad general de Einstein nos enseña lo que sucede en el mundo más grande, el de las estrellas y galaxias.

Había algunos inconvenientes. Los electrones, como hemos dicho, seguían la mecánica cuántica ondulatoria de Schrödinger. No obstante, cuando los electrones adquieren velocidades muy altas, cercanas a la velocidad de la luz, los efectos de la relatividad especial empiezan a tener importancia.

La ecuación de Schrödinger describe partículas cuánticas NO relativistas.

Como Einstein nos enseñó, el espacio y el tiempo son caras de la misma moneda, el espacio-tiempo. La ecuación de Schrödinger trata el espacio y el tiempo de forma distinta ya que el tiempo se encuentra en una derivada parcial de orden 1, en cambio el espacio se encuentra en forma de derivada parcial de orden 2.

¿Entonces cómo podemos describir partículas cuánticas relativistas?

Paul Dirac fue quien solucionó este problema convirtiendo la ecuación ondulatoria de Schrödinger en una ecuación relativista. Todos conocemos la famosa ecuación de Einstein E=mc^2, seguramente la ecuación más famosa de la historia.

Pues resulta que podemos fusionar esta ecuación con la ecuación de Schrödinger obteniendo la ecuación de Klein-Gordon que describe el comportamiento de una partícula cuántica con efectos relativistas.

Sin embargo, esta expresión tenia ciertos problemas. Esta expresión tiene la derivada respecto el tiempo al cuadrado.

Como sabemos de matemáticas básicas una ecuación de orden 2 tiene dos soluciones. En este caso, la segunda ecuación representa una energía negativa.

Pero… ¿Qué representa físicamente una energía negativa?

Otro problema de la ecuación de Klein-Gordon es que se obtienen probabilidades negativas con la función de onda al cuadrado. Pero como sabemos por Max Born, el cuadrado de la función de onda representa la probabilidad de encontrar la partícula en una región definida.

Por lo tanto, las probabilidades negativas no tienen ningún sentido físico real.

¿Qué hizo Dirac para solucionar estos problemas?

Fácil, quitó los cuadrados de la ecuación y problema resuelto.

Bueno… en realidad es mucho más complejo que eso.

Pensó una expresión matemática que al cuadrado fuera equivalente a la ecuación de Klein-Gordon.

Esta nueva ecuación dependía de unos parámetros que Dirac encontró que eran matrices.

Ahora viene la magia…

Estas matrices 4x4 (matrices de Dirac) tenían implícitas las famosas matrices de Pauli.

¿No sabes que son las matrices de Pauli?

Madre mía…

Bueno pues las matrices de Pauli son la representación irreducible del grupo de Lie SU(2). Un grupo de simetría que describe el spin de una partícula.

¿Aún no entiendes nada?

Vamos a hacerlo más fácil…

Las matrices de Pauli son los objetos matemáticos que describen el spin de las partículas cuánticas.

¿Mejor?

Continuamos…

Dirac dijo que el spin no es más que la consecuencia de aplicar las leyes relativistas en el mundo cuántico.

En esta ecuación la función de onda ya no tiene las propiedades de un vector. Estas diferentes propiedades describen a un objeto matemático más complejo, un espinor.

El espinor que describe la función de onda es una matriz columna con 4 componentes. Esto nos da dos resultados. Una de ellas con energía negativa.

¿Cómo se interpreta esto?

Dirac interpretó este resultado como soluciones que pertenecen a partículas análogas con carga opuesta a la partícula original. Él las llamo antipartículas.

Pues sí…

De la ecuación de Dirac nace de forma natural la antimateria. Años más tarde se demostró experimentalmente la existencia de antielectrones conocidos como positrones. Más adelante también se confirmó la existencia de antineutrones y antiprotones.

¿Te das cuenta de todo lo que implica esta bella y hermosa ecuación?

Hemos visto que es la ecuación de Dirac y algunas de sus implicaciones en la física moderna. Pero si aun no has tenido suficiente y te va lo “hardcore” ahora empezaremos con la parte interesante. La formulación matemática de la ecuación más bella de la historia, la formula de Dirac.

A la izquierda de la ecuación tenemos la ecuación relativista de energía: E^2 = p^2c^2+m^2+c^4 y la derecha la definición de operador energía de la ecuación de Schrödinger.

De esta forma se obtiene la ecuación de Klein-Gordon. Sin embargo, como hemos mencionado previamente esta expresión presenta ciertas dificultades incompatibles con los fundamentos de la mecánica cuántica.

El truco que aplicó Dirac (como vemos en la siguiente ecuación) fue encontrar una expresión matemática que al cuadrado fuera equivalente a la ecuación de Klein-Gordon.

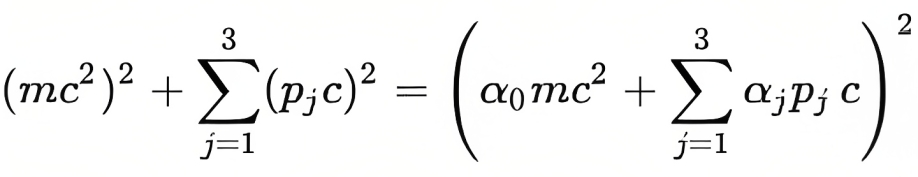
Esta expresión depende de dos parámetros que Dirac encontró que eran matrices y no números reales o complejos.

Desarrollando las ecuaciones y utilizando la notación relativista covariante llegamos a la famosa ecuación de Dirac: (∂ - m) ψ = 0.

La ecuación relativista para la energía en principio acepta tanto energías positivas como energías negativas.

Pero… ¿Qué es una energía negativa?

Por nuestra experiencia, no existen las energías negativas, pero Dirac, dio una interesante explicación que resolvería esta aparente imposible solución negativa.

Él decía que el vacío tendría todos los estados energéticos negativos ocupados. Este modelo se conoce como el océano o mar de Dirac el cual considera el estado del vacío como un mar infinito de electrones con energía negativa.

Cualquier electrón extra tendría ocupar un estado energético positivo ya que el principio de exclusión de Pauli prohíbe que dos fermiones ocupen el mismo estado cuántico.

Más adelante Dirac dijo que si no estuvieran todos completos habría un “hueco” en uno de los estados de energía negativa y este se comportaría como una partícula de carga positiva.

Esta partícula era el positrón (la antipartícula del electrón) que posteriormente fue descubierta experimentalmente por Carl David Anderson.