Entropía de Shannon

La entropía de Shannon es un es un importante concepto de la teoría de la información con múltiples aplicaciones en ciencias de la computación, en telecomunicaciones y como no podía ser menos, en deep learning.
Un concepto muy relacionado con la entropía de Shannon es “crossentropy” o entropía cruzada. Esta medida es usualmente utilizada como función de perdida en múltiples arquitecturas de redes neuronales.
Este artículo tiene como objetivo dar una breve introducción al lector de la teoría de la información y de la medida de entropía en relación a dicha teoría. Además, veremos otros conceptos muy importantes como la entropía cruzada o la divergencia de Kullback-Leibler.
Concepto de entropía
El concepto de entropía aparece en muchos ámbitos de la ciencia y tecnología. En física estadística la entropía es considerada como el grado de desorden de un sistema.

Qué es el overfitting
El overfitting o sobreajuste es uno de los problemas más comunes en el mundo de la estadística y del machine learning. Aprende a detectarlo y solucionarlo.
Ver artículoNo obstante, esta definición es imprecisa. La definición real de entropía es el grado de información/desinformación que tenemos de un sistema. Es decir, cuanta más información tengamos menos entropía.
Pongamos un ejemplo. Cuando el agua se encuentra a una temperatura de -273,15 ºC (el cero absoluto) las moléculas no se mueven en absoluto. Por lo tanto, solo tiene una configuración posible y la información que tenemos de dicho sistema es máxima. Por eso, este sistema ideal tendría una entropía de cero.
Si aumentamos la temperatura del agua, las moléculas adoptaran múltiples configuraciones disminuyendo la cantidad de información a la cual podemos acceder y, por lo tanto, aumentando la entropía.
En la teoría de la información, la entropía se refiere a la cantidad de información que nos aporta un evento o distribución de probabilidad. Seguidamente entraremos en más detalle.
La entropía en la teoría de la información
Como hemos visto, la entropía de Shannon mide la cantidad de información de una distribución de probabilidad o evento. Por ejemplo, imaginemos que vivimos en una ciudad donde siempre llueve. La información “mañana lloverá” no nos aporta mucha información nueva ya que cada día llueve.
Otros posts que te gustarán
No obstante, si el mensaje dice “Mañana hará un sol radiante” nos aporta mucha más información ya que es un evento que es poco probable que sucede. Por lo tanto, este último evento tiene una mayor entropía que el anterior.
La entropía es un concepto básico en teoria de la información. Sin embargo, en machine learning y en otros campos de la estadística como la inferencia variacional, otros conceptos relacionados como la entropía cruzada o la divergencia de Kullback-Leibler (Entropía relativa) son más importantes.
Entropía cruzada o “cross-entropy”
La entropía cruzada mide la diferencia entre dos distribuciones de probabilidad de un conjunto de eventos.
En muchas áreas de la inteligencia artificial esta medida se usa como función de coste (cost function) o función de perdida (loss function).
Al final, el objetivo de muchas tareas de deep learning es construir una función de probabilidad sobre la variable de interés que se aproxime al máximo a la distribución real. Para saber la diferencia entre la distribución inferida y la real (la cual proviene del conjunto de entrenamiento) se utiliza la medida de cross-entropy.
A cada iteración, el cross-entropy se minimiza reduciendo el error y obteniendo cada vez un modelo que se aproxime al máximo a la distribución real de probabilidad.
A nivel matemático, la cross-entropy se define como la entropía de la distribución real p más la diferencia entre la distribución real y la modelada. Si estas dos distribuciones de probabilidad son las mismas, entonces, la entropía y la entropía cruzada son equivalentes. Este segundo término se conoce como divergencia de Kullback-Leibler, KL-divergence o entropía relativa:
H(p,q) = H(p) + DKL(p|q)
En deep learning, como veremos en la siguiente sección, la entropía se mantiene constante. Por lo tanto, minimizar la entropía cruzada es equivalente a minimizar la entropía relativa.
Divergencia Kullback-Leibler o entropía relativa
Otro concepto importante es la divergencia de Kullback-Leibler. Esta medida está relacionada matemáticamente con la entropía cruzada.
Divergencia = entropía cruzada – entropía
Esta medida, igual que la entropía cruzada, nos indica cuanto de diferente es la distribución generada por el modelo de la distribución real.
En el contexto del machine learning y deep learning la divergencia de Kullback-Leibler y la cross-entropy son equivalentes ya que como vemos en la ecuación, lo único que les diferencia es la entropía. Esta entropía esta definida sobre la distribución de probabilidad real, por lo tanto, no cambia y podemos obviarla.
Aplicaciones de la entropía de Shannon en Machine Learning
En machine learning, más concretamente en problemas de clasificación, la entropía cruzada es utilizada como función de coste.
Imaginemos que queremos entrenar una red neuronal convolucional que sea capaz de generar un multiclasificador que, dada una imagen de un animal, nos indique a que animal pertenece dicha foto.
Al final de la arquitectura de un multiclasificador generado con una CNN (Convolutional Neural Network) tenemos una función softmax que nos indica las probabilidades que tiene la foto de pertenecer a cada una de las categorías.
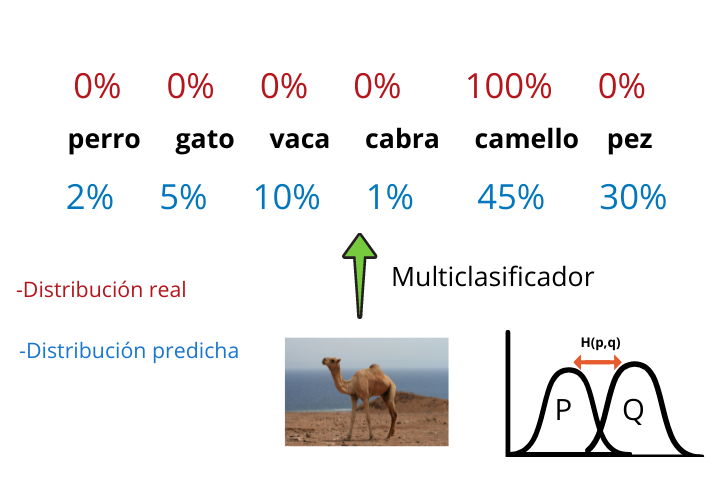
Finalmente se coge la etiqueta que tiene la probabilidad más alta y se muestra el resultado.
Esta distribución de probabilidad generada por el multiclasificador es la distribución modelada q y los resultados reales (que los tenemos ya que estamos trabajando con aprendizaje supervisado) forman la distribución real p.
Construyendo la función de entropía cruzada y minimizándola a cada iteración iremos reduciendo la diferencia entre ambas distribuciones y por lo tanto nuestro modelo generara resultados cada vez más reales.

