O que é raiz quadrada média do erro RMSE e MSE

No aprendizado de máquina e mais especificamente no aprendizado supervisionado, é importante ter uma métrica que indique o erro que nosso modelo apresenta. Existem diferentes métricas que nos dão uma ideia de quão bom ou ruim é o nosso modelo de previsão.

Um deles é o MSE (Erro Quadrático Médio) ou o RMSE (Erro Quadrático Médio). O segundo difere do primeiro porque a raiz quadrada é usada para obter as unidades do problema em vez de elevá-las ao quadrado.

O cálculo do MSE ou RMSE consiste em comparar os valores reais com os previstos pelo modelo. Esta comparação é feita através da distância euclidiana de ambos os valores.

Na imagem a seguir podemos ver uma regressão linear (linha azul) e os pontos de dados reais (cor amarela). Para cada ponto vemos uma linha vermelha que se conecta ao ponto do modelo, neste caso com a linha de regressão linear. A linha vermelha representa a distância euclidiana entre os dois pontos. Isto é calculado operando a norma na diferença dos valores.

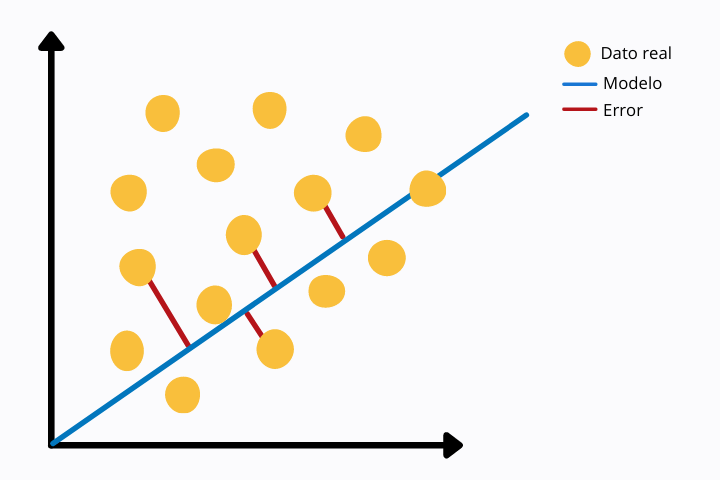
Essa métrica de erro é mais sensível a valores discrepantes, pois estamos usando uma potência. Outras medidas menos sensíveis a outliers são, por exemplo, o MAE ou Erro Médio Absoluto em que o valor absoluto é obtido sem ser elevado ao quadrado.

Durante o treinamento do modelo de aprendizado de máquina em aprendizado supervisionado, em cada iteração é calculada uma função de erro que é então minimizada através de algoritmos de otimização com o objetivo de reduzir o erro e melhorar o resultado a cada iteração.

Existem múltiplas funções de erro (também conhecidas como funções de custo). Um deles é o MSE ou erro quadrático médio.

Esta função tem a forma de uma parábola, portanto possui apenas um mínimo global. Esse recurso o torna ideal para algoritmos de minimização, pois eles encontrarão mais facilmente o valor global que minimiza o erro sem ficarem presos em outros mínimos locais.

O RMSE é mais intuitivo que o MSE, mas a nível computacional é mais caro. Na aprendizagem supervisionada, como arquiteturas de redes neurais, o erro deve ser calculado em cada iteração. Por esta razão, como o RMSE é mais caro, é preferível utilizar o MSE como função de custo.

Outra razão é que o algoritmo de otimização gradiente descendente tem melhor desempenho em MSE do que em RMSE.

Como vimos, MAE é uma métrica de erro muito semelhante ao MSE ou RMSE. O MAE é mais robusto que o RMSE e, portanto, não dá tanta importância aos outliers. Caso contrário, o RMSE, ao elevar o valor absoluto da diferença ao quadrado, dá mais importância aos outliers.

RMSE e MSE são funções diferenciáveis, portanto podem ser utilizadas em problemas de otimização. Além disso, em cada ponto o gradiente é diferente, ou seja, a primeira derivada em relação à função de erro varia ponto a ponto. Isto não acontece no caso da função MAE onde o gradiente é o mesmo em cada ponto, exceto em zero onde não é diferenciável. A função derivada não é contínua em todo o domínio.

Isso pode causar problemas no treinamento do modelo, principalmente quando utilizamos redes neurais.

Em alguns problemas é possível que nem RMSE, MSE ou MAE nos ajudem. Neste caso teremos que procurar alternativas. Uma delas é a função de perda conhecida como função de Huber.

É uma função por partes que é robusta a valores discrepantes e diferenciável de 0, ao contrário do MAE.

A função Huber possui um parâmetro delta ajustável que deve ser ajustado dependendo do problema de interesse.

Outra alternativa às funções de custo tradicionais é a função Log-Cosh. Isso é semelhante ao erro quadrático médio, com a diferença de que é mais suave, tornando-o menos sensível a valores discrepantes.

Além disso, a função é duplamente diferenciável, ao contrário da função de Huber, que só é diferenciável uma vez.

Por possuir derivada dupla, a função Log-Cosh pode ser utilizada por métodos de otimização de segunda ordem, como o método de Newton-Raphson, utilizado em técnicas de otimização. aumento de gradiente como XGBoost.