Equação de Dirac, descubra o significado desta fórmula que mistura quantum com relatividade

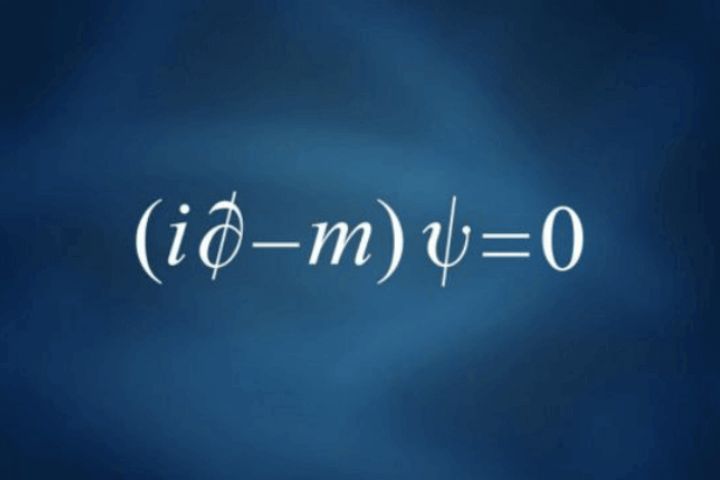
A equação de Dirac, também conhecida como equação do amor ou a equação mais bonita do mundo por sua simplicidade, é uma equação fundamental da física que combina a mecânica quântica e a teoria da relatividade para descrever partículas com spin 1/2, como os elétrons, levando em consideração os efeitos relativísticos e prevendo a existência de antipartículas.

Quer descobrir mais sobre esta linda fórmula?

Fique conosco e descubra porque Paul Dirac foi um dos grandes físicos do século XX!

Durante o século 20, surgiram duas das teorias mais influentes da física moderna: a relatividade geral e a mecânica quântica. Essas duas belas teorias nos permitem descrever a maioria dos fenômenos físicos do nosso universo.

As leis da mecânica quântica nos explicam o que acontece no menor mundo, o mundo atômico e subatômico. Em vez disso, a relatividade geral de Einstein ensina-nos o que acontece no mundo mais vasto, o das estrelas e das galáxias.

Houve algumas desvantagens. Os elétrons, como dissemos, seguiram a mecânica quântica ondulatória de Schrödinger. Porém, quando os elétrons adquirem velocidades muito elevadas, próximas à velocidade da luz, os efeitos da relatividade especial começam a ser importantes.

A equação de Schrödinger descreve partículas quânticas NÃO relativísticas.

Como Einstein nos ensinou, espaço e tempo são faces da mesma moeda, espaço-tempo. A equação de Schrödinger trata o espaço e o tempo de forma diferente, uma vez que o tempo está numa derivada parcial de ordem 1, enquanto o espaço está na forma de uma derivada parcial de ordem 2.

Então, como podemos descrever partículas quânticas relativísticas?

Paul Dirac foi quem resolveu este problema convertendo a equação de onda de Schrödinger em uma equação relativística. Todos conhecemos a famosa equação de Einstein E=mc^2, certamente a equação mais famosa da história.

Bom, acontece que podemos fundir esta equação com a equação de Schrödinger, obtendo a equação de Klein-Gordon que descreve o comportamento de uma partícula quântica com efeitos relativísticos.

No entanto, esta expressão teve alguns problemas. Esta expressão tem a derivada em relação ao tempo ao quadrado.

Como sabemos pela matemática básica, uma equação de ordem 2 tem duas soluções. Neste caso, a segunda equação representa uma energia negativa.

Mas... O que a energia negativa representa fisicamente?

Outro problema com a equação de Klein-Gordon é que probabilidades negativas são obtidas com a função de onda quadrada. Mas como sabemos por Max Born, o quadrado da função de onda representa a probabilidade de encontrar a partícula numa região definida.

Portanto, as probabilidades negativas não têm significado físico real.

O que Dirac fez para resolver esses problemas?

Fácil, removi os quadrados da equação e problema resolvido.

Bem… na verdade é muito mais complexo que isso.

Ele pensou em uma expressão matemática cujo quadrado seria equivalente à equação de Klein-Gordon.

Esta nova equação dependia de parâmetros que Dirac descobriu serem matrizes.

Agora vem a magia...

Essas matrizes 4x4 (matrizes de Dirac) tinham implícitas as famosas matrizes de Pauli.

Você não sabe o que são matrizes de Pauli?

Minha mãe…

Bem, as matrizes de Pauli são a representação irredutível do grupo de Lie SU(2). Um grupo de simetria que descreve o spin de uma partícula.

Ainda não entendeu nada?

Vamos facilitar...

Matrizes de Pauli são os objetos matemáticos que descrevem o spin das partículas quânticas.

Melhorar?

Nós continuamos…

Dirac disse que o spin nada mais é do que a consequência da aplicação de leis relativísticas no mundo quântico.

Nesta equação a função de onda não possui mais as propriedades de um vetor. Essas diferentes propriedades descrevem um objeto matemático mais complexo, um espinor.

O espinor que descreve a função de onda é uma matriz coluna com 4 componentes. Isso nos dá dois resultados. Um deles com energia negativa.

Como isso é interpretado?

Dirac interpretou este resultado como soluções pertencentes a partículas análogas com carga oposta à da partícula original. Ele os chamou de antipartículas.

Pois sim…

A antimatéria nasce naturalmente da equação de Dirac. Anos mais tarde, a existência de antielétrons conhecidos como pósitrons foi demonstrada experimentalmente. Mais tarde também foi confirmada a existência de antinêutrons e antiprótons.

Você percebe tudo o que essa linda e bela equação implica?

Vimos o que é a equação de Dirac e algumas de suas implicações na física moderna. Mas se você ainda não se cansou e gosta de hardcore, agora começaremos com a parte interessante. A formulação matemática da equação mais bela da história, a fórmula de Dirac.

À esquerda da equação temos a equação relativística da energia: E^2 = p^2c^2+m^2+c^4 e à direita a definição do operador energia da equação de Schrödinger.

Desta forma, a equação de Klein-Gordon é obtida. Porém, como mencionamos anteriormente, esta expressão apresenta certas dificuldades incompatíveis com os fundamentos da mecânica quântica.

O truque que Dirac aplicou (como vemos na equação a seguir) foi encontrar uma expressão matemática cujo quadrado fosse equivalente à equação de Klein-Gordon.

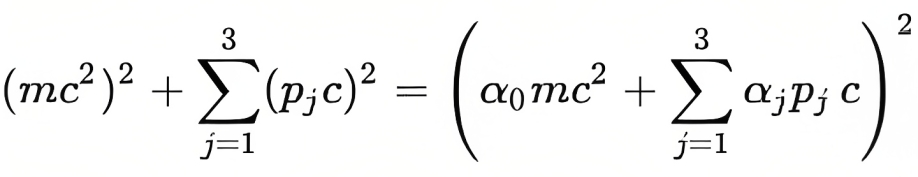
Esta expressão depende de dois parâmetros que Dirac descobriu serem matrizes e não números reais ou complexos.

Desenvolvendo as equações e utilizando a notação relativística covariante chegamos à famosa equação de Dirac: (∂ - m) ψ = 0.

A equação relativística da energia, em princípio, aceita tanto energias positivas como energias negativas.

Mas... O que é energia negativa?

Na nossa experiência, não existem energias negativas, mas Dirac deu uma explicação interessante que resolveria esta solução negativa aparentemente impossível.

Ele disse que o vazio teria todos os estados de energia negativa ocupados. Este modelo é conhecido como oceano ou mar de Dirac, que considera o estado do vácuo como um mar infinito de elétrons com energia negativa.

Qualquer elétron extra teria que ocupar um estado de energia positivo, uma vez que o princípio de exclusão de Pauli proíbe dois férmions de ocuparem o mesmo estado quântico.

Mais tarde, Dirac disse que se não estivessem todos completos, haveria uma “lacuna” em um dos estados de energia negativa e esta se comportaria como uma partícula carregada positivamente.

Esta partícula era o pósitron (a antipartícula do elétron) que mais tarde foi descoberta experimentalmente por Carl David Anderson.