Curvas ROC

Cuando usamos modelos estadísticos y más concretamente técnicas de machine learning, uno de los puntos clave para interpretar los resultados correctamente es elegir la métrica adecuada para medir el error del modelo.

En modelos de clasificación, una de las métricas más usadas para comprobar la fiabilidad es la curva ROC (Receiver Operating Characteristic).

Esta métrica de error mide la capacidad del modelo para clasificar correctamente los positivos en distintos umbrales o thresholds.

Recomendado

Qué es un árbol de decisión

¿Quieres aprender qué son los árboles de decisión y qué aplicaciones tienen en el mundo del machine learning supervisado? Entra y descubre estos modelos.

Ver artículo

Cuando entrenamos un modelo de clasificación binario queremos saber si una instancia es positivo o negativa. Pongamos un ejemplo:

Imagina que queremos entrenar un modelo de machine learning que sea capaz de clasificar si un correo electrónico tiene un virus o no. Lo que obtendremos como resultado es la probabilidad de que un correo tenga virus.

Normalmente, si la probabilidad está por encima de 0.5 lo clasificamos como positivo (tiene un virus) y si está por debajo los clasificamos como negativo (no tiene un virus).

No obstante, si quisiéramos aumentar el porcentaje de correos clasificados como que tienen un virus que realmente tiene un virus podríamos subir el umbral. De esta forma nos aseguramos que si decimos que el email es maligno entonces es muy probable que lo sea.

Sin embargo, habría otros que tendrían virus informático que no estaríamos capturando. Subiendo el umbral mejoramos lo que se conoce como precisión del modelo.

En cambio, si bajamos el umbral, mejoraríamos el porcentaje de emails clasificados como malignos que realmente lo son. En este caso estaríamos aumentando el recall del modelo.

La medida ROC indica la ratio de positivos reales versus la ratio de positivos falsos en distintos umbrales de clasificación.

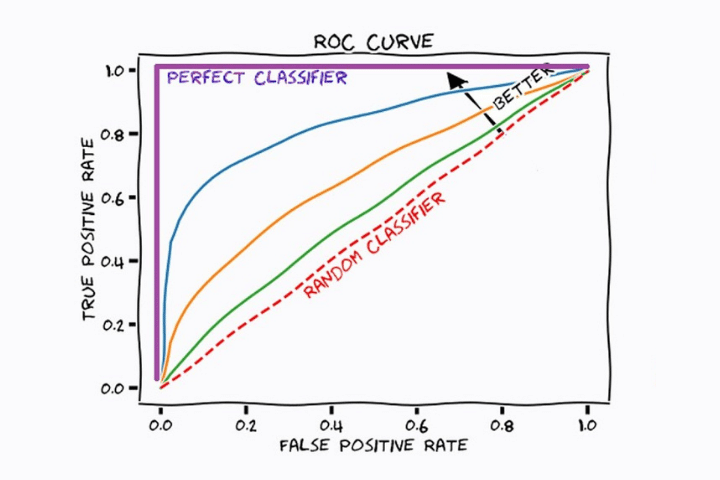
En la siguiente imagen vemos un gráfico con distintas curvas. Cada una de ellas corresponde a un modelo de machine learning de clasificación distinto. La línea recta roja indica el resultado de un modelo que clasifica las muestras de forma aleatoria.

En todas las curvas vemos que a medida que aumenta la ratio de positivos reales (recall) aumenta el número de falsos positivos. Esto es porque esta disminuyendo el umbral y por lo tanto la mayoría de positivos serán clasificados como positivos, pero algunos negativos también serán clasificados como positivos.

El modelo óptimo será aquél que aumente más rápida el valor del eje de coordenadas (TPR) mientras mantiene un valor bajo en el eje de abscisas (FPR). En este caso el modelo estadístico correspondiente al color azul (sin tener en cuenta el color morado que sería el ideal) es el más adecuado.

Hemos visto en secciones anteriores que la forma de la curva nos indica cual es el mejor modelo de clasificación. No obstante, de forma visual puede resultar un poco complicado. Por esta razón, lo mejores es encontrar un valor numérico que nos indique de forma cuantitativa cual de los modelos entrenados de clasificación es el que mejor se adapta a nuestro problema.

Aquí entra la AUC o área bajo la curva. Se trata de un simple cálculo integral de la superficie que se encuentra debajo de la curva del modelo. Un modelo perfecto tendría un AUC de 1 y un modelo pésimo tendría un valor de 0.

Esta métrica nos permite comparar diferentes modelos y optar por el que mejor clasifica nuestra muestra.

El uso de ROC y AUC es conocido cómo método ROC-AUC.

Veamos algunos ejemplos:

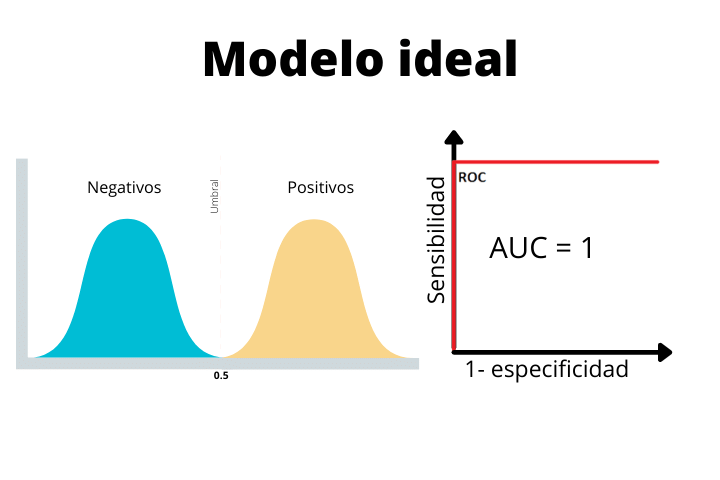
En la primera imagen vemos el caso de un modelo ideal con una curva en forma de escalón y un área bajo la curva (AUC) de 1. Este es un caso perfecto y nunca lo obtendremos como resultado final con datos reales. Si en un problema real obtienes dicha curva es muy recomendable sospechar ya que un modelo tan perfecto no es común.

Vemos como en el modelo ideal, las dos distribuciones están perfectamente separadas por el umbral. Al no existir solapación, el modelo será capaz de clasificar perfectamente las muestras.

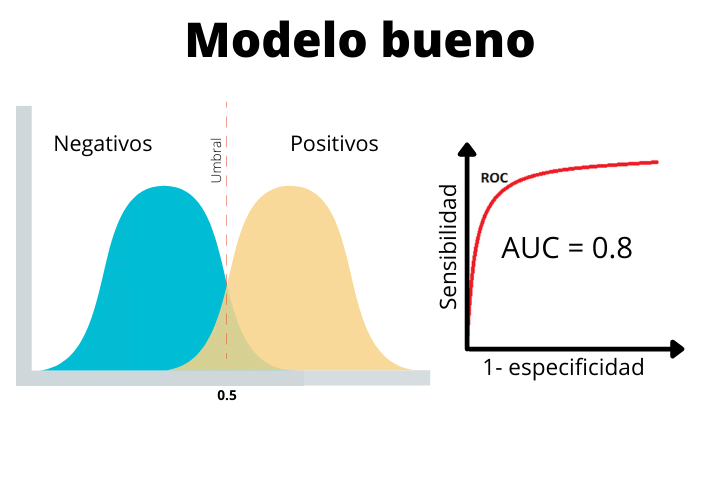
En el segundo caso vemos un modelo real con una AUC de 0.8. Este tipo de curva es la que esperamos en un problema real típico de clasificación. Como vemos, las dos distribuciones se solapan un poco. Esto hará que tengamos algunos falsos positivos y algunos falsos negativos.

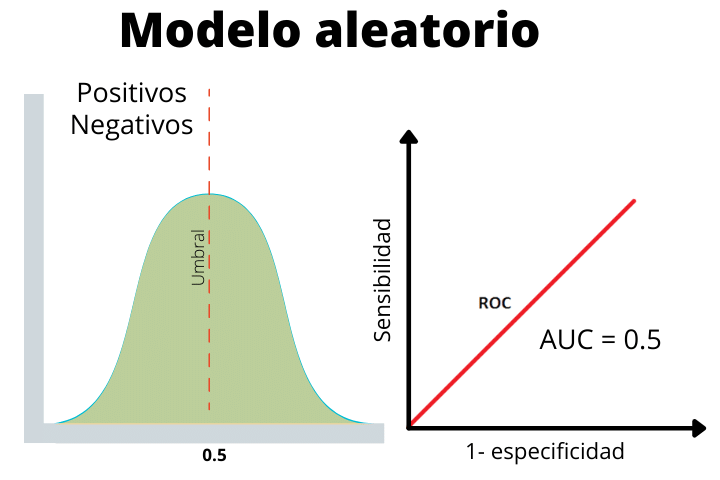
Finalmente tenemos el caso de un modelo aleatorio donde las etiquetas de positivo y negativo se han dado al azar. Esta recta nos sirve para determinar si el rendimiento de nuestro modelo es superior al esperado de forma aleatorio o inferior.

Como vemos, las dos distribuciones se solapan, por lo tanto, no es capaz de discernir entre un positivo o un negativo.