Curvas ROC

Quando utilizamos modelos estatísticos e mais especificamente técnicas de aprendizado de máquina, um dos pontos-chave para interpretar corretamente os resultados é escolher a métrica adequada para medir o erro do modelo.

Nos modelos de classificação, uma das métricas mais utilizadas para verificar a confiabilidade é a curva ROC (Receiver Operating Characteristic).

Esta métrica de erro mede a capacidade do modelo de classificar corretamente os positivos em diferentes limites.

Quando treinamos um modelo de classificação binária queremos saber se uma instância é positiva ou negativa. Vejamos um exemplo:

Imagine que queremos treinar um modelo de aprendizado de máquina que seja capaz de classificar se um e-mail contém vírus ou não. O que obteremos como resultado é a probabilidade de um e-mail conter vírus.

Normalmente, se a probabilidade estiver acima de 0,5 classificamos como positivo (tem vírus) e se estiver abaixo classificamos como negativo (não tem vírus).

No entanto, se quiséssemos aumentar a percentagem de e-mails classificados como contendo vírus que realmente contêm vírus, poderíamos aumentar o limite. Desta forma garantimos que se dissermos que o e-mail é malicioso, é muito provável que seja.

No entanto, haveria outros que teriam vírus de computador que não estaríamos detectando. Ao aumentar o limite, melhoramos o que é conhecido como precisão do modelo.

Por outro lado, se diminuirmos o limite, melhoraremos a percentagem de e-mails classificados como maliciosos que realmente o são. Nesse caso estaríamos aumentando o recall do modelo.

A medida ROC indica a proporção de verdadeiros positivos versus a proporção de falsos positivos em diferentes limites de classificação.

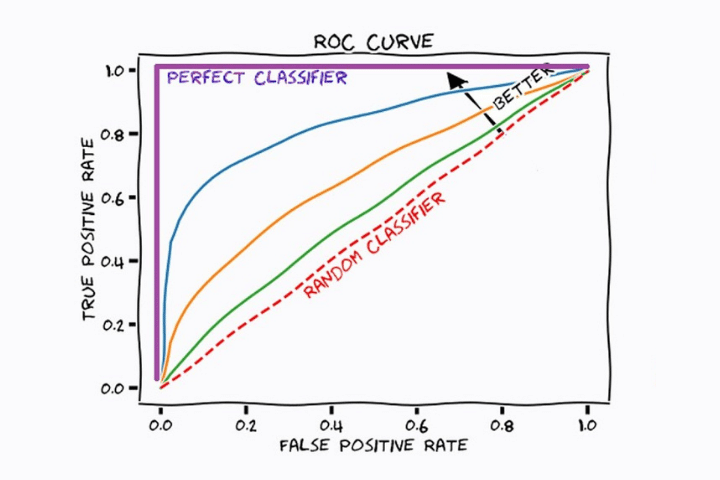
Na imagem a seguir vemos um gráfico com diferentes curvas. Cada um deles corresponde a um modelo de aprendizado de máquina de classificação diferente. A linha reta vermelha indica o resultado de um modelo que classifica as amostras aleatoriamente.

Em todas as curvas vemos que à medida que a proporção de verdadeiros positivos (recall) aumenta, o número de falsos positivos aumenta. Isso ocorre porque o limite está diminuindo e, portanto, a maioria dos positivos será classificada como positiva, mas alguns negativos também serão classificados como positivos.

O modelo ideal será aquele que aumenta o valor do eixo de coordenadas (TPR) mais rapidamente, mantendo um valor baixo no eixo x (FPR). Neste caso, o modelo estatístico correspondente à cor azul (sem levar em conta a cor roxa, que seria o ideal) é o mais adequado.

Vimos nas seções anteriores que o formato da curva nos diz qual é o melhor modelo de classificação. No entanto, visualmente pode ser um pouco complicado. Por esta razão, é melhor encontrar um valor numérico que nos diga quantitativamente qual dos modelos de classificação treinados melhor se adapta ao nosso problema.

Aí vem a AUC ou área sob a curva. Este é um cálculo integral simples da área de superfície sob a curva do modelo. Um modelo perfeito teria uma AUC de 1 e um modelo ruim teria um valor de 0.

Esta métrica permite-nos comparar diferentes modelos e optar por aquele que melhor classifica a nossa amostra.

O uso de ROC e AUC é conhecido como método ROC-AUC.

Vejamos alguns exemplos:

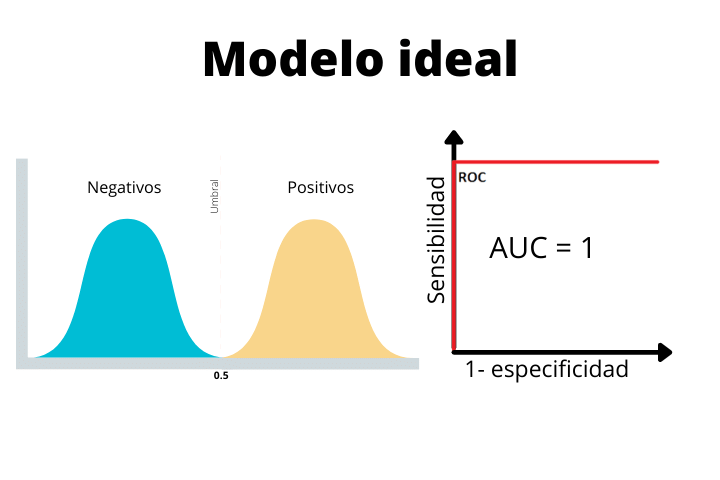
Na primeira imagem vemos o caso de um modelo ideal com uma curva escalonada e uma área sob a curva (AUC) de 1. Este é um caso perfeito e nunca o obteremos como resultado final com dados reais. Se você obtiver tal curva em um problema real, é altamente recomendável suspeitar, pois um modelo tão perfeito não é comum.

Vemos como no modelo ideal as duas distribuições estão perfeitamente separadas pelo limite. Como não há sobreposição, o modelo será capaz de classificar as amostras perfeitamente.

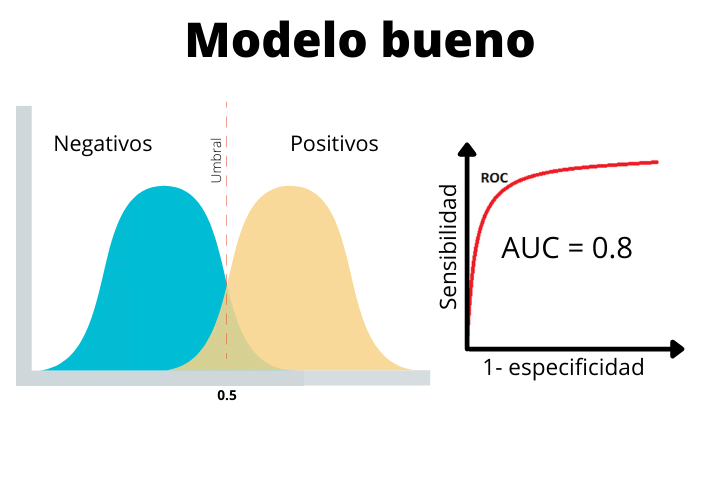
No segundo caso vemos um modelo real com AUC de 0,8. Este tipo de curva é o que esperamos em um problema típico de classificação do mundo real. Como podemos ver, as duas distribuições se sobrepõem um pouco. Isso fará com que tenhamos alguns falsos positivos e alguns falsos negativos.

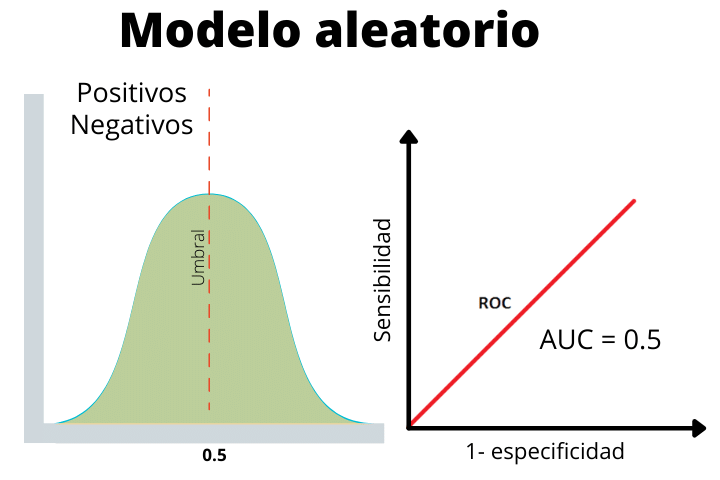
Finalmente temos o caso de um modelo aleatório onde os rótulos positivos e negativos foram dados aleatoriamente. Esta linha nos ajuda a determinar se o desempenho do nosso modelo é superior ao esperado aleatoriamente ou inferior.

Como vemos, as duas distribuições se sobrepõem, portanto, não é possível discernir entre uma positiva ou uma negativa.