Qu'est-ce que l'erreur quadratique moyenne RMSE et MSE

En apprentissage automatique et plus particulièrement en apprentissage supervisé, il est important de disposer d'une métrique qui indique l'erreur de notre modèle. Il existe différentes mesures qui nous donnent une idée de la qualité ou de la mauvaise qualité de notre modèle de prédiction.

L’un d’eux est le MSE (Mean Squared Error) ou le RMSE (Root Mean Squared Error). La seconde diffère de la première en ce sens que la racine carrée est utilisée pour obtenir les unités du problème au lieu de les mettre au carré.

Le calcul du MSE ou du RMSE consiste à comparer les valeurs réelles avec celles prédites par le modèle. Cette comparaison se fait grâce à la distance euclidienne des deux valeurs.

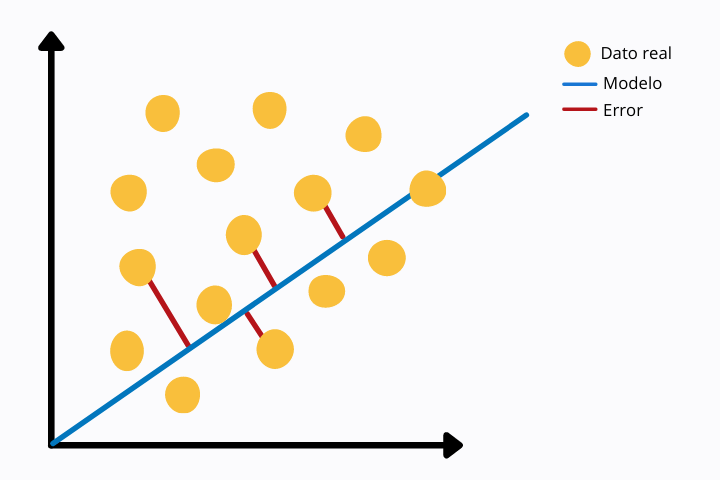
Dans l'image suivante, nous pouvons voir une régression linéaire (ligne bleue) et les points de données réels (couleur jaune). Pour chaque point, nous voyons une ligne rouge qui se connecte au point du modèle, dans ce cas avec la ligne de régression linéaire. La ligne rouge représente la distance euclidienne entre les deux points. Celui-ci est calculé en opérant la norme sur la différence des valeurs.

Cette métrique d'erreur est plus sensible aux valeurs aberrantes puisque nous utilisons une puissance. D'autres mesures moins sensibles aux valeurs aberrantes sont, par exemple, la MAE ou Mean Absolute Error dans laquelle la valeur absolue est prise sans la mettre au carré.

Lors de l'entraînement du modèle d'apprentissage automatique en apprentissage supervisé, à chaque itération une fonction d'erreur est calculée qui est ensuite minimisée grâce à des algorithmes d'optimisation dans le but de réduire l'erreur et d'améliorer le résultat à chaque itération.

Il existe plusieurs fonctions d'erreur (également appelées fonctions de coût). L’un d’eux est le MSE ou Mean Square Error.

Cette fonction a la forme d’une parabole et n’a donc qu’un minimum global. Cette fonctionnalité le rend idéal pour les algorithmes de minimisation car ils trouveront plus facilement la valeur globale qui minimise l'erreur sans se laisser piéger par d'autres minima locaux.

Le RMSE est plus intuitif que le MSE, mais au niveau informatique, il est plus coûteux. Dans l'apprentissage supervisé tel que les architectures de réseaux de neurones, l'erreur doit être calculée à chaque itération. Pour cette raison, puisque le RMSE est plus cher, il est préférable d’utiliser le MSE comme fonction de coût.

Une autre raison est que l'algorithme d'optimisation de descente de gradient a de meilleures performances sur MSE que sur RMSE.

Comme nous l'avons vu, MAE est une métrique d'erreur très similaire à MSE ou RMSE. MAE est plus robuste que RMSE et n’accorde donc pas autant d’importance aux valeurs aberrantes. Sinon, le RMSE, en élevant la valeur absolue de la différence au carré, donne plus d'importance aux valeurs aberrantes.

RMSE et MSE sont des fonctions différentiables et peuvent donc être utilisées dans des problèmes d'optimisation. De plus, en chaque point le gradient est différent, c'est-à-dire que la dérivée première par rapport à la fonction d'erreur varie point par point. Cela n'arrive pas dans le cas de la fonction MAE où le gradient est le même en chaque point, sauf en zéro où il n'est pas dérivable. La fonction dérivée n'est pas continue dans tout le domaine.

Cela peut poser des problèmes lors de la formation du modèle, notamment lorsque nous utilisons des réseaux de neurones.

Dans certains problèmes, il est possible que ni RMSE, MSE ou MAE ne nous aident. Dans ce cas, nous devrons chercher des alternatives. L’une d’elles est la fonction de perte connue sous le nom de fonction de Huber.

Il s'agit d'une fonction par morceaux qui est robuste aux valeurs aberrantes et différentiable à 0 contrairement à MAE.

La fonction Huber possède un paramètre delta réglable qui doit être ajusté en fonction du problème qui vous intéresse.

Une autre alternative aux fonctions de coût traditionnelles est la fonction Log-Cosh. Ceci est similaire à l’erreur quadratique moyenne, à la différence qu’elle est plus douce, ce qui la rend moins sensible aux valeurs aberrantes.

De plus, la fonction est doublement différentiable contrairement à la fonction de Huber qui n'est différentiable qu'une seule fois.

Comme elle possède une dérivée double, la fonction Log-Cosh peut être utilisée par des méthodes d'optimisation du second ordre, comme la méthode de Newton-Raphson, utilisée dans les techniques d'optimisation. augmentation du dégradé comme XGBoost.