Équation de Dirac, découvrez le sens de cette formule qui mêle quantique et relativité

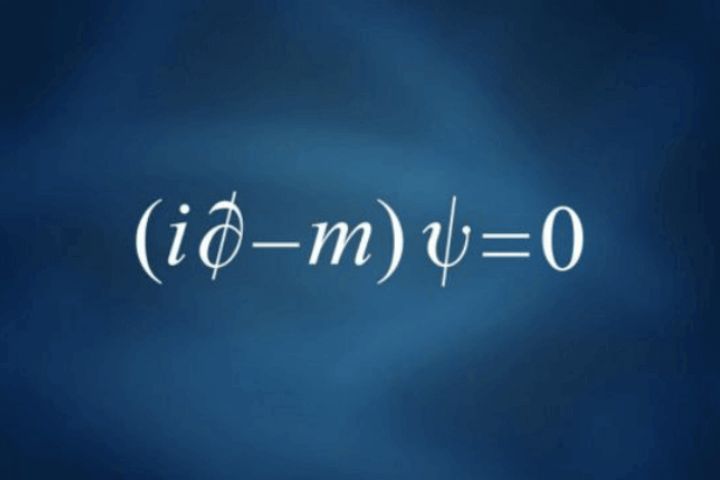
L'équation de Dirac, également connue sous le nom d'équation d'amour ou la plus belle équation du monde pour sa simplicité, est une équation fondamentale en physique qui combine la mécanique quantique et la théorie de la relativité pour décrire les particules de spin 1/2, comme les électrons, en tenant compte des effets relativistes et en prédisant l'existence d'antiparticules.

Vous souhaitez en savoir plus sur cette belle formule ?

Restez avec nous et découvrez pourquoi Paul Dirac a été l'un des grands physiciens du 20ème siècle !

Au cours du XXe siècle, deux des théories les plus influentes de la physique moderne ont émergé : la relativité générale et la mécanique quantique. Ces deux belles théories nous permettent de décrire la majorité des phénomènes physiques de notre univers.

Les lois de la mécanique quantique nous expliquent ce qui se passe dans le plus petit monde, le monde atomique et subatomique. Au lieu de cela, la relativité générale d'Einstein nous enseigne ce qui se passe dans le monde plus vaste, celui des étoiles et des galaxies.

Il y avait quelques inconvénients. Les électrons, comme nous l'avons dit, ont suivi la mécanique quantique ondulatoire de Schrödinger. Cependant, lorsque les électrons acquièrent des vitesses très élevées, proches de la vitesse de la lumière, les effets de la relativité restreinte commencent à être importants.

L'équation de Schrödinger décrit des particules quantiques NON relativistes.

Comme Einstein nous l’a enseigné, l’espace et le temps sont les faces d’une même pièce, l’espace-temps. L'équation de Schrödinger traite l'espace et le temps différemment puisque le temps est dans une dérivée partielle d'ordre 1, tandis que l'espace est sous la forme d'une dérivée partielle d'ordre 2.

Alors, comment pouvons-nous décrire les particules quantiques relativistes ?

C'est Paul Dirac qui a résolu ce problème en convertissant l'équation des ondes de Schrödinger en une équation relativiste. Nous connaissons tous la célèbre équation d'Einstein E=mc^2, sûrement l'équation la plus célèbre de l'histoire.

Eh bien, il s'avère que nous pouvons fusionner cette équation avec l'équation de Schrödinger, obtenant ainsi l'équation de Klein-Gordon qui décrit le comportement d'une particule quantique avec des effets relativistes.

Cependant, cette expression présentait certains problèmes. Cette expression a la dérivée par rapport au temps carré.

Comme nous le savons grâce aux mathématiques de base, une équation d’ordre 2 a deux solutions. Dans ce cas, la deuxième équation représente une énergie négative.

Mais... Que représente physiquement l'énergie négative ?

Un autre problème avec l'équation de Klein-Gordon est que des probabilités négatives sont obtenues avec la fonction d'onde carrée. Mais comme nous le sait Max Born, le carré de la fonction d’onde représente la probabilité de trouver la particule dans une région définie.

Par conséquent, les probabilités négatives n’ont aucune signification physique réelle.

Qu’a fait Dirac pour résoudre ces problèmes ?

Facile, supprimez les carrés de l’équation et le problème est résolu.

Eh bien… c'est en fait beaucoup plus complexe que ça.

Il a pensé à une expression mathématique dont le carré serait équivalent à l'équation de Klein-Gordon.

Cette nouvelle équation dépendait de paramètres que Dirac considérait comme des matrices.

Maintenant vient la magie...

Ces matrices 4x4 (matrices de Dirac) avaient implicitement les fameuses matrices de Pauli.

Vous ne savez pas ce que sont les matrices de Pauli ?

Ma mère…

Eh bien, les matrices de Pauli sont la représentation irréductible du groupe de Lie SU(2). Un groupe de symétrie qui décrit le spin d'une particule.

Vous ne comprenez toujours rien ?

Rendons les choses plus faciles...

Les matrices de Pauli sont les objets mathématiques qui décrivent le spin des particules quantiques.

Mieux?

Nous continuons…

Dirac a déclaré que le spin n'est rien d'autre que la conséquence de l'application des lois relativistes dans le monde quantique.

Dans cette équation, la fonction d’onde n’a plus les propriétés d’un vecteur. Ces différentes propriétés décrivent un objet mathématique plus complexe, un spineur.

Le spineur qui décrit la fonction d’onde est une matrice colonne à 4 composantes. Cela nous donne deux résultats. L’un d’eux avec une énergie négative.

Comment cela est-il interprété ?

Dirac a interprété ce résultat comme des solutions appartenant à des particules analogues de charge opposée à la particule d'origine. Il les appelait des antiparticules.

Hé bien oui…

L'antimatière est née naturellement de l'équation de Dirac. Des années plus tard, l’existence d’antiélectrons appelés positrons a été démontrée expérimentalement. Plus tard, l'existence d'antineutrons et d'antiprotons a également été confirmée.

Réalisez-vous tout ce que cette belle et belle équation implique ?

Nous avons vu ce qu'est l'équation de Dirac et certaines de ses implications dans la physique moderne. Mais si vous n'en avez toujours pas assez et que vous aimez le hardcore, nous allons maintenant commencer par la partie intéressante. La formulation mathématique de la plus belle équation de l’histoire, la formule de Dirac.

A gauche de l'équation nous avons l'équation énergétique relativiste : E^2 = p^2c^2+m^2+c^4 et à droite la définition de l'opérateur énergétique de l'équation de Schrödinger.

De cette manière, l'équation de Klein-Gordon est obtenue. Cependant, comme nous l’avons évoqué précédemment, cette expression présente certaines difficultés incompatibles avec les fondements de la mécanique quantique.

L’astuce appliquée par Dirac (comme nous le voyons dans l’équation suivante) consistait à trouver une expression mathématique dont le carré était équivalent à l’équation de Klein-Gordon.

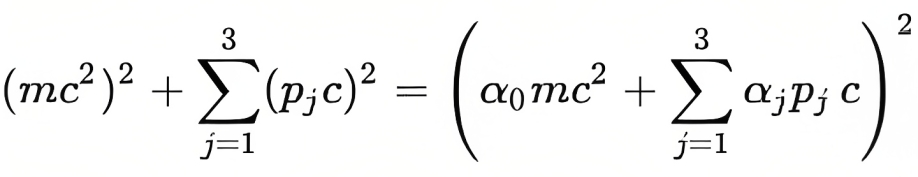
Cette expression dépend de deux paramètres que Dirac a trouvés être des matrices et non des nombres réels ou complexes.

En développant les équations et en utilisant la notation relativiste covariante nous arrivons à la célèbre équation de Dirac : (∂ - m) ψ = 0.

L’équation relativiste de l’énergie accepte en principe à la fois les énergies positives et les énergies négatives.

Mais... Qu'est-ce que l'énergie négative ?

D’après notre expérience, les énergies négatives n’existent pas, mais Dirac a donné une explication intéressante qui résoudrait cette solution négative apparemment impossible.

Il a dit que le vide occuperait tous les états d’énergie négative. Ce modèle est connu sous le nom d'océan ou mer de Dirac, qui considère l'état du vide comme une mer infinie d'électrons à énergie négative.

Tout électron supplémentaire devrait occuper un état d’énergie positif puisque le principe d’exclusion de Pauli interdit à deux fermions d’occuper le même état quantique.

Plus tard, Dirac a déclaré que s’ils n’étaient pas tous complets, il y aurait un « écart » dans l’un des états d’énergie négative et celui-ci se comporterait comme une particule chargée positivement.

Cette particule était le positron (l’antiparticule de l’électron) qui fut découvert expérimentalement par Carl David Anderson.