Courbes ROC

Lorsque nous utilisons des modèles statistiques et plus spécifiquement des techniques d’apprentissage automatique, l’un des points clés pour interpréter correctement les résultats est de choisir la métrique appropriée pour mesurer l’erreur du modèle.

Dans les modèles de classification, l'une des métriques les plus utilisées pour vérifier la fiabilité est la courbe ROC (Receiver Operating Characteristic).

Cette mesure d'erreur mesure la capacité du modèle à classer correctement les positifs à différents seuils.

Lorsque nous formons un modèle de classification binaire, nous voulons savoir si une instance est positive ou négative. Prenons un exemple :

Imaginez que nous souhaitions former un modèle d'apprentissage automatique capable de déterminer si un e-mail contient un virus ou non. Le résultat que nous obtiendrons est la probabilité qu'un e-mail contienne un virus.

Normalement, si la probabilité est supérieure à 0,5, nous la classons comme positive (il a un virus) et si elle est inférieure, nous la classons comme négative (il n'a pas de virus).

Cependant, si nous voulions augmenter le pourcentage d’e-mails classés comme contenant un virus qui contiennent réellement un virus, nous pourrions augmenter le seuil. De cette façon, nous garantissons que si nous disons que l'e-mail est malveillant, il est très probable qu'il le soit.

Cependant, il y en aurait d’autres qui contiendraient des virus informatiques que nous ne pourrions pas détecter. En augmentant le seuil, nous améliorons ce que l'on appelle la précision du modèle.

En revanche, si nous abaissons le seuil, nous améliorerions le pourcentage d’e-mails classés comme malveillants qui le sont réellement. Dans ce cas, nous augmenterions le rappel du modèle.

La mesure ROC indique le ratio de vrais positifs par rapport au ratio de faux positifs à différents seuils de classification.

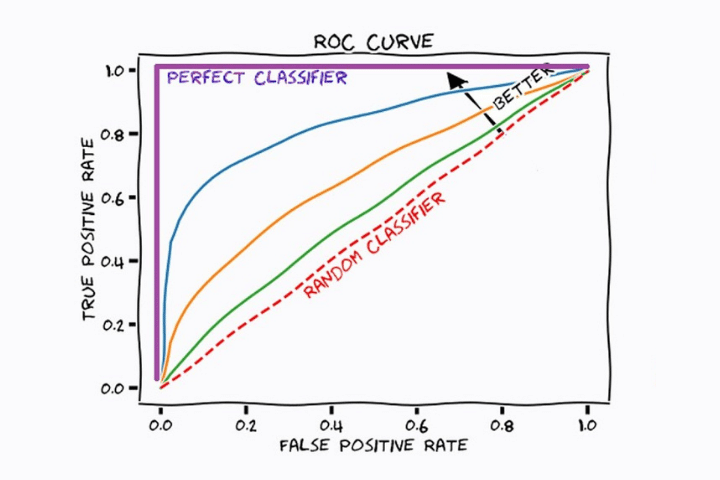
Dans l'image suivante, nous voyons un graphique avec différentes courbes. Chacun d’eux correspond à un modèle d’apprentissage automatique de classification différent. La ligne droite rouge indique le résultat d'un modèle qui classe les échantillons de manière aléatoire.

Dans toutes les courbes, nous constatons que plus le ratio de vrais positifs (rappel) augmente, plus le nombre de faux positifs augmente. En effet, le seuil diminue et donc la plupart des positifs seront classés comme positifs, mais certains négatifs seront également classés comme positifs.

Le modèle optimal sera celui qui augmente le plus rapidement la valeur de l'axe des coordonnées (TPR) tout en conservant une valeur faible sur l'axe des x (FPR). Dans ce cas, le modèle statistique correspondant à la couleur bleue (sans tenir compte de la couleur violette, qui serait l'idéal) est le plus approprié.

Nous avons vu dans les sections précédentes que la forme de la courbe nous indique quel est le meilleur modèle de classification. Cependant, visuellement, cela peut être un peu compliqué. Pour cette raison, il est préférable de trouver une valeur numérique qui nous indique quantitativement lequel des modèles de classification formés s'adapte le mieux à notre problème.

Voici l'AUC ou l'aire sous la courbe. Il s'agit d'un simple calcul intégral de la surface sous la courbe du modèle. Un modèle parfait aurait une AUC de 1 et un modèle médiocre aurait une valeur de 0.

Cette métrique nous permet de comparer différents modèles et d'opter pour celui qui classe le mieux notre échantillon.

L’utilisation de ROC et AUC est connue sous le nom de méthode ROC-AUC.

Regardons quelques exemples :

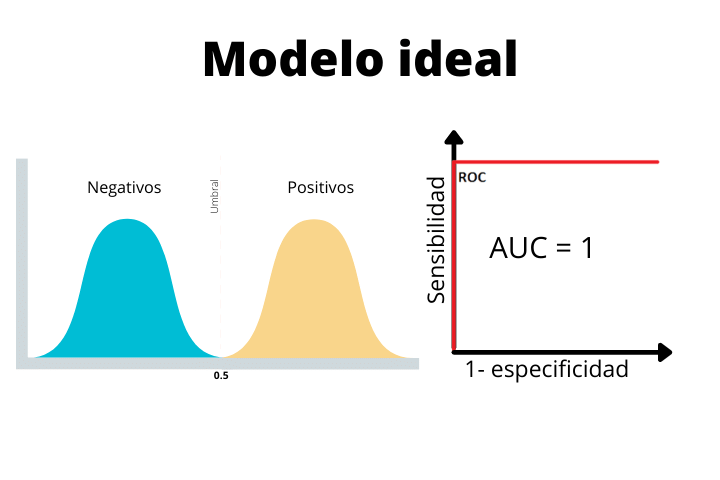
Dans la première image, nous voyons le cas d'un modèle idéal avec une courbe en forme de gradins et une aire sous la courbe (AUC) de 1. C'est un cas parfait et nous ne l'obtiendrons jamais comme résultat final avec des données réelles. Si l’on obtient une telle courbe dans un problème réel, il est fortement conseillé de se méfier car un modèle aussi parfait n’est pas courant.

On voit comment dans le modèle idéal, les deux distributions sont parfaitement séparées par le seuil. Puisqu’il n’y a pas de chevauchement, le modèle pourra parfaitement classer les échantillons.

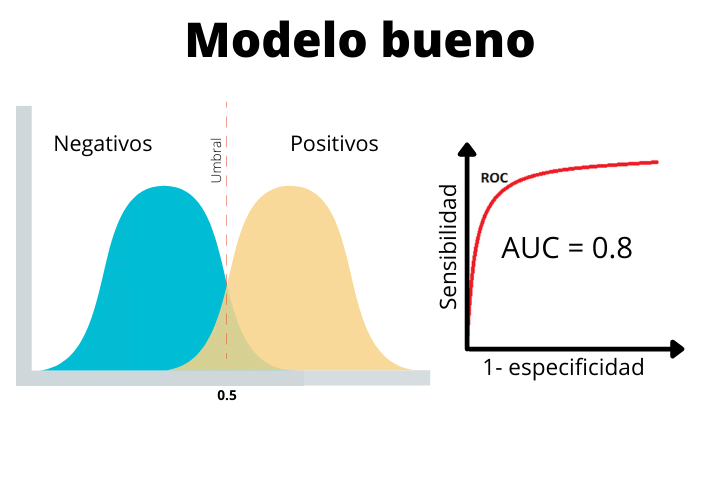
Dans le deuxième cas, nous voyons un modèle réel avec une AUC de 0,8. Ce type de courbe est ce à quoi nous nous attendons dans un problème de classification typique du monde réel. Comme on le voit, les deux distributions se chevauchent un peu. Cela nous amènera à avoir des faux positifs et des faux négatifs.

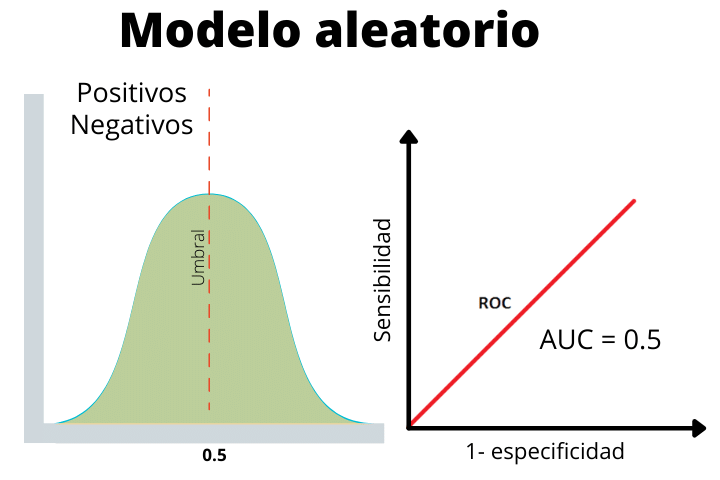
Enfin nous avons le cas d'un modèle aléatoire où les étiquettes positives et négatives ont été données aléatoirement. Cette ligne nous aide à déterminer si les performances de notre modèle sont supérieures aux attentes de manière aléatoire ou inférieures.

Comme nous le voyons, les deux distributions se chevauchent, il n’est donc pas possible de distinguer un positif d’un négatif.