Entropia de Shannon

A entropia de Shannon é um conceito importante na teoria da informação com múltiplas aplicações em ciência da computação, telecomunicações e, claro, aprendizagem profunda.

Um conceito intimamente relacionado à entropia de Shannon é “crossentropia”. Esta medida é geralmente usada como uma função de perda em múltiplas arquiteturas de redes neurais.

Este artigo tem como objetivo dar ao leitor uma breve introdução à teoria da informação e à medição da entropia em relação a essa teoria. Além disso, veremos outros conceitos muito importantes como entropia cruzada ou divergência de Kullback-Leibler.

O conceito de entropia aparece em muitas áreas da ciência e da tecnologia. Na física estatística, a entropia é considerada o grau de desordem de um sistema.

No entanto, esta definição é imprecisa. A verdadeira definição de entropia é o grau de informação/desinformação que temos sobre um sistema. Ou seja, quanto mais informação tivermos, menos entropia.

Vejamos um exemplo. Quando a água está a uma temperatura de -273,15 ºC (zero absoluto) as moléculas não se movem. Portanto, só possui uma configuração possível e as informações que temos sobre o referido sistema são máximas. Portanto, este sistema ideal teria uma entropia zero.

Se aumentarmos a temperatura da água, as moléculas adotarão múltiplas configurações, diminuindo a quantidade de informação que podemos acessar e, portanto, aumentando a entropia.

Na teoria da informação, entropia refere-se à quantidade de informação que um evento ou distribuição de probabilidade nos fornece. Entraremos em mais detalhes abaixo.

Como vimos, a entropia de Shannon mede a quantidade de informação numa probabilidade ou distribuição de eventos. Por exemplo, vamos imaginar que moramos em uma cidade onde chove sempre. A informação “choverá amanhã” não nos dá muitas informações novas, pois chove todos os dias.

Porém, se a mensagem disser “Amanhã fará muito sol”, isso nos dá muito mais informações, pois é um evento que provavelmente não acontecerá. Portanto, este último evento possui uma entropia maior que o anterior.

Entropia é um conceito básico na teoria da informação. No entanto, no aprendizado de máquina e em outros campos da estatística, como a inferência variacional, outros conceitos relacionados, como entropia cruzada ou divergência de Kullback-Leibler (entropia relativa), são mais importantes.

A entropia cruzada mede a diferença entre duas distribuições de probabilidade de um conjunto de eventos.

Em muitas áreas da inteligência artificial esta medida é usada como função de custo ou função de perda.

No final, o objetivo de muitas tarefas de aprendizagem profunda é construir uma função de probabilidade na variável de interesse que seja o mais próxima possível da distribuição real. Para saber a diferença entre a distribuição inferida e a real (que vem do conjunto de treinamento), utiliza-se a medida de entropia cruzada.

A cada iteração, a entropia cruzada é minimizada reduzindo o erro e obtendo cada vez um modelo o mais próximo possível da distribuição de probabilidade real.

A nível matemático, a entropia cruzada é definida como a entropia da distribuição real p mais a diferença entre a distribuição real e a modelada. Se essas duas distribuições de probabilidade forem iguais, então a entropia e a entropia cruzada são equivalentes. Este segundo termo é conhecido como divergência de Kullback-Leibler, divergência KL ou entropia relativa:

H(p,q) = H(p) + DKL(p|q)

Na aprendizagem profunda, como veremos na próxima seção, a entropia permanece constante. Portanto, minimizar a entropia cruzada equivale a minimizar a entropia relativa.

Outro conceito importante é a divergência de Kullback-Leibler. Esta medida está matematicamente relacionada à entropia cruzada.

Divergência = entropia cruzada – entropia

Esta medida, tal como a entropia cruzada, diz-nos quão diferente é a distribuição gerada pelo modelo da distribuição real.

No contexto do aprendizado de máquina e do aprendizado profundo, a divergência de Kullback-Leibler e a entropia cruzada são equivalentes, pois, como vemos na equação, a única coisa que os diferencia é a entropia. Esta entropia é definida na distribuição de probabilidade real, portanto, não muda e podemos ignorá-la.

No aprendizado de máquina, mais especificamente em problemas de classificação, a entropia cruzada é utilizada como função de custo.

Vamos imaginar que queremos treinar uma rede neural convolucional que seja capaz de gerar um multiclassificador que, dada a imagem de um animal, nos diga a qual animal pertence aquela foto.

Ao final da arquitetura de um multiclassificador gerado com uma CNN (Rede Neural Convolucional) temos uma função softmax que nos informa as probabilidades que a foto tem de pertencer a cada uma das categorias.

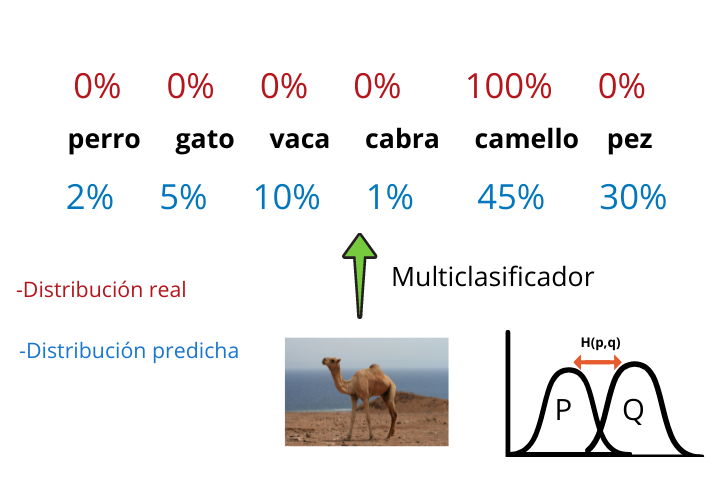
Por fim, o rótulo com maior probabilidade é obtido e o resultado é exibido.

Essa distribuição de probabilidade gerada pelo multiclassificador é a distribuição modelada q e os resultados reais (que temos já que estamos trabalhando com aprendizagem supervisionada) formam a distribuição real p.

Ao construir a função de entropia cruzada e minimizá-la a cada iteração, reduziremos a diferença entre as duas distribuições e, portanto, nosso modelo gerará resultados cada vez mais realistas.