Entropie de Shannon

L'entropie de Shannon est un concept important de la théorie de l'information avec de multiples applications en informatique, en télécommunications et, bien sûr, en apprentissage profond.

Un concept étroitement lié à l’entropie de Shannon est la « crossentropie ». Cette mesure est généralement utilisée comme fonction de perte dans plusieurs architectures de réseaux neuronaux.

Cet article vise à donner au lecteur une brève introduction à la théorie de l'information et à la mesure de l'entropie en relation avec ladite théorie. De plus, nous verrons d’autres concepts très importants comme l’entropie croisée ou la divergence de Kullback-Leibler.

Le concept d’entropie apparaît dans de nombreux domaines scientifiques et technologiques. En physique statistique, l’entropie est considérée comme le degré de désordre d’un système.

Cependant, cette définition est imprécise. La véritable définition de l’entropie est le degré d’information/désinformation dont nous disposons sur un système. Autrement dit, plus nous avons d’informations, moins il y a d’entropie.

Prenons un exemple. Lorsque l’eau est à une température de -273,15 ºC (zéro absolu), les molécules ne bougent pas du tout. Par conséquent, il n’a qu’une seule configuration possible et les informations dont nous disposons sur ledit système sont maximales. Ce système idéal aurait donc une entropie nulle.

Si nous augmentons la température de l’eau, les molécules adopteront de multiples configurations, diminuant la quantité d’informations auxquelles nous pouvons accéder et augmentant ainsi l’entropie.

En théorie de l’information, l’entropie fait référence à la quantité d’informations que nous fournit un événement ou une distribution de probabilité. Nous y reviendrons plus en détail ci-dessous.

Comme nous l'avons vu, l'entropie de Shannon mesure la quantité d'informations dans une distribution de probabilité ou d'événement. Par exemple, imaginons que nous vivions dans une ville où il pleut toujours. L'information « il pleuvra demain » ne nous apporte pas beaucoup d'informations nouvelles puisqu'il pleut tous les jours.

Cependant, si le message dit « Demain, il fera beau », cela nous donne beaucoup plus d’informations car il s’agit d’un événement peu probable. Ce dernier événement a donc une entropie plus élevée que le précédent.

L'entropie est un concept fondamental de la théorie de l'information. Cependant, dans l'apprentissage automatique et dans d'autres domaines statistiques tels que l'inférence variationnelle, d'autres concepts connexes tels que l'entropie croisée ou la divergence Kullback-Leibler (entropie relative) sont plus importants.

L'entropie croisée mesure la différence entre deux distributions de probabilité d'un ensemble d'événements.

Dans de nombreux domaines de l’intelligence artificielle, cette mesure est utilisée comme fonction de coût ou fonction de perte.

En fin de compte, l’objectif de nombreuses tâches d’apprentissage profond est de construire une fonction de probabilité sur la variable d’intérêt qui soit aussi proche que possible de la distribution réelle. Pour connaître la différence entre la distribution déduite et la distribution réelle (qui provient de l'ensemble d'apprentissage), la mesure d'entropie croisée est utilisée.

A chaque itération, l'entropie croisée est minimisée en réduisant l'erreur et en obtenant à chaque fois un modèle le plus proche possible de la distribution de probabilité réelle.

Au niveau mathématique, l'entropie croisée est définie comme l'entropie de la distribution réelle p plus la différence entre la distribution réelle et celle modélisée. Si ces deux distributions de probabilité sont identiques, alors l'entropie et l'entropie croisée sont équivalentes. Ce deuxième terme est connu sous le nom de divergence Kullback-Leibler, divergence KL ou entropie relative :

H(p,q) = H(p) + DKL(p|q)

En deep learning, comme nous le verrons dans la section suivante, l’entropie reste constante. Par conséquent, minimiser l’entropie croisée équivaut à minimiser l’entropie relative.

Un autre concept important est la divergence Kullback-Leibler. Cette mesure est mathématiquement liée à l'entropie croisée.

Divergence = entropie croisée – entropie

Cette mesure, comme l'entropie croisée, nous indique à quel point la distribution générée par le modèle est différente de la distribution réelle.

Dans le contexte de l’apprentissage automatique et de l’apprentissage profond, la divergence de Kullback-Leibler et l’entropie croisée sont équivalentes puisque, comme on le voit dans l’équation, la seule chose qui les différencie est l’entropie. Cette entropie est définie sur la distribution de probabilité réelle, elle ne change donc pas et on peut l'ignorer.

En apprentissage automatique, plus spécifiquement dans les problèmes de classification, l'entropie croisée est utilisée comme fonction de coût.

Imaginons que nous souhaitions former un réseau de neurones convolutifs capable de générer un multiclassificateur qui, étant donné l'image d'un animal, nous indique à quel animal appartient la photo.

A la fin de l'architecture d'un multiclassificateur généré avec un CNN (Convolutional Neural Network) nous avons une fonction softmax qui indique les probabilités qu'a la photo d'appartenir à chacune des catégories.

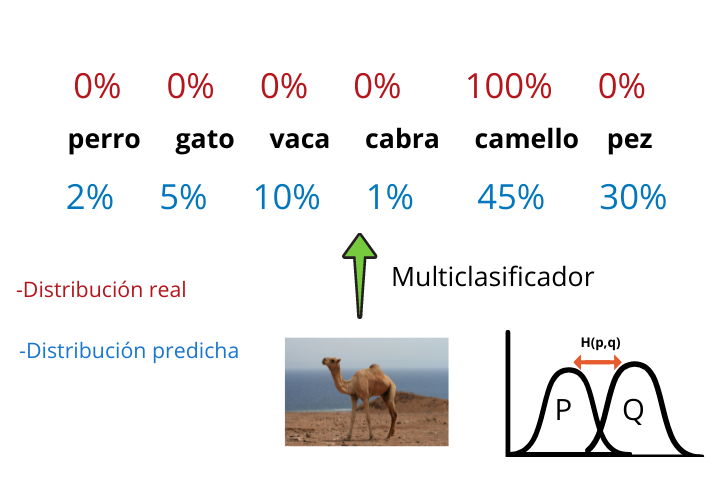
Enfin, l'étiquette ayant la probabilité la plus élevée est prise et le résultat est affiché.

Cette distribution de probabilité générée par le multiclassificateur est la distribution modélisée q et les résultats réels (que nous avons puisque nous travaillons avec l'apprentissage supervisé) forment la distribution réelle p.

En construisant la fonction d'entropie croisée et en la minimisant à chaque itération, nous réduirons la différence entre les deux distributions et donc notre modèle générera des résultats de plus en plus réalistes.